【読みやすいコードのガイドライン】変数の直交性

2026-01-16

Kotlin

はじめに

この記事は書籍「読みやすいコードのガイドライン」¹について読んで学んだことをまとめた記事です。数学で書かれている部分については著者の完全な感想というか、専門分野外なので、そんなに真正面から見ないでください（笑）

変数の直交性

定義

2つの変数について、それぞれのの値の取りうる範囲（変域）がもう一方の値に影響されない場合、それらの変数は互いに直交の関係にある

直交でないことを非直交ということにします。

数学のベクトルにおける直交性

ベクトルの直交の単純な例は、ベクトル $\mathbf{v}$ とベクトル $\mathbf{w}$ が直交する場合、

\mathbf{v} \cdot \mathbf{w} = 0

を満たすことです。またその空間の次元と同じ数のベクトルがそれぞれ直交であれば、その空間の任意のベクトルはそれらのベクトルの線形結合で表すことができます。

コードにおける直交性の例

class OwnedCoinScreen {
    private var ownedCoins: Int = ...
    private var isTransactionHistoryShown: Boolean = ...
}

このコードには2つのプロパティが宣言されていて、それぞれ変数です。ownedCoinsは所有するコインを表し、isTransactionHistoryShownはUI上で履歴を表示するかどうかを表します。なんのコインがいくらあろうが、UIの履歴を開閉することが可能なはずです。逆にあるAに対するコインが100の時に、UIが開閉できなかったら明確なバグです。よって、これら2つの変数は独立であり、直交する関係にあると言えます。

ownedCoinsはIntであり、その範囲は $\mathtt{ownedCoins} \in \mathbb{N}$ です（現実のお金であればここは非負が期待されるでしょうが、コード上はそこまで制限していないです）。isTransactionHistoryShownはBooleanであり、その範囲は $\mathtt{isTransactionHistoryShown} \in \{\mathtt{true}, \mathtt{false}\}$ です。よって、このクラスの空間は

\mathtt{OwnedCoinScreen} \cong \mathbb{N}_{\geq 0} \times \{\mathtt{true}, \mathtt{false}\}

であると言えます。つまり、この空間は

\mathtt{OwnedCoinScreen} \cong \mathtt{Int} \times \mathtt{Boolean}

という関係のように見えます。

コードにおける非直交の例

class CoinDisplayModel {
    val ownedCoins: Int, 
    val ownedCoinText: String
}

これはコインの数ownedCoinsと、表示するテキストownedCoinTextを表すクラスです。これは

CoinDisplayModel(1, "1 coin")
CoinDisplayModel(2, "2 coins")

が想定通りですが、

CoinDisplayModel(1, "2 coins")
CoinDisplayModel(2, "1 coin")

は想定外の値となります。違いの変数に依存して不具合が生じるなら、それは直交ではありません。これは

\mathtt{CoinDisplayModel} \subseteq \mathtt{Int} \times \mathtt{String}

であると言えます。

暗黙的にownedCoinTextはownedCoinsに依存しているので、

\begin{align} \mathtt{ownedCoinText} = f(\mathtt{ownedCoins}) \end{align}

のような関数があるべきです。

非直交のコードを書き換える

式 $(1)$ を満たすようにCoinDisplayModelを書き換えると、

data CoinDisplayModel(val ownedCoins: Int) {
    fun getOwnedCoinText(): String {
        val suffixx = if (ownedCoins == 1) "coin" else "coins"
        return "$ownedCoins $suffixx"
    }
}

もし、ownendCoinTextの計算コストが高いとき、毎回計算するのではなく、計算結果を保持しておきたいときがあります。その場合、

class CoinDisplayModel {
    var ownedCoins: Int
        private set
    var ownedCoinText: String
        private set

    fun updateOwnedCoins(newCoinCount: Int) {
        ownedCoins = newCoinCount
        ownedCoinText = createOwnedCoinText(ownedCoins)
    }

    companion object {
        fun createOwnedCoinText(ownedCoins: Int): String {
            // this.ownedCoinsは参照できないので、間違って更新しようとしてもコンパイルエラーしてくれる
            val ownedCoinText = ... // `ownedCoins`に依存する計算
            return ownedCoinText
        }
    }
}

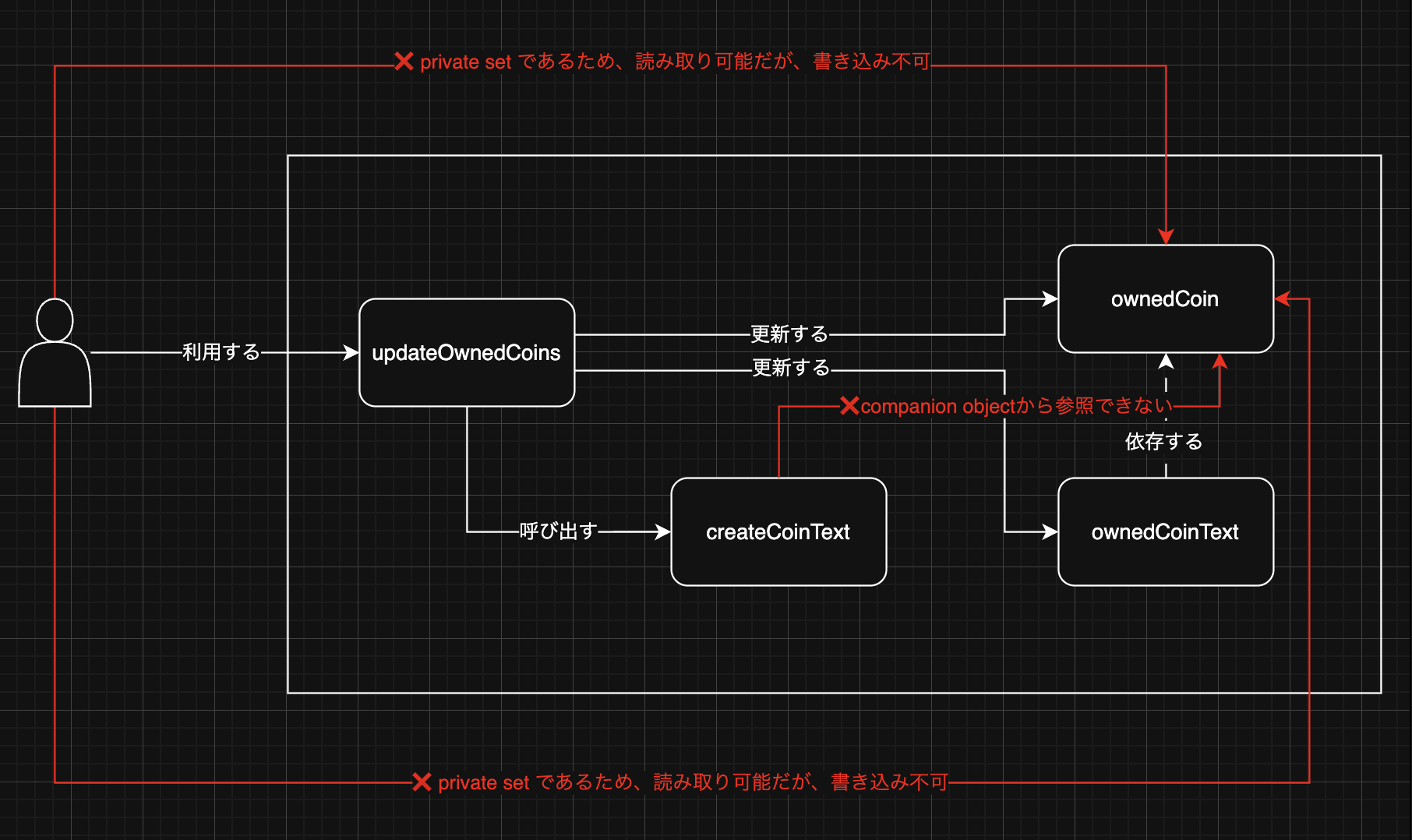
と書かれます。

なぜ`companion object`で書く必要があるのか？

companion object²は静的(static)なメソッドを表すために用います。ここで、動的と静的について述べておきます。動的とは、ここでは $`ownedCoins`のようにインスタンスごとに変わりうる量です。静的であるというのは、インスタンスごとに変わらないという意味で、例えば`ownedCoinText`のように`ownedCoins`を受け取って`"$ {this.ownedCoins} coins"`のように表すメソッドであるとすると、このメソッドはインスタンスの違いに依存しません。

また、companion objectで書くことで、companion objectのメソッド自体が外側のスコープの変数を更新することがないことが保証されます。またprivate装飾子をつけることで、外部からも遮断された独立性の高いメソッドになります。

ひとこと

直交性という名前は誤解を生みそうです。直積のほうが近い概念だと思いました。まる。