超幾何分布

定義

2種類$A, B$からなる$N$個のものがあり、それぞれ$M, N - M$個ある。この集団から勝手に$n$個取り出したときに、$A$が$x$個、$B$が$n - x$個であるとする。 $x$の最小値は

1. $0$（ただし$n \leq N -M$）
2. $n - (N - M)$（ただし$n > N - M$）

$x$の最大値は

1. $n$（ただし$n < M$）
2. $M$（ただし$n \geq M$）

です。実は上記の最小値の大小関係について¹にtypoの疑いがあります。最小値について等号が成立するのが、私は1のほうだと考えていますが、参考¹の方は2の方に等号が付きます。

例として$N = 7, M = 3$の場合を考えてみます。$A$と$B$の物体をそれぞれ$a$と$b$と表すことにします。すると

$$a \quad a \quad a \quad b \quad b \quad b \quad b$$

のように並べることができるでしょう。$n < N - M = 4$だとすると、$n = 3$まで物体をとることになります。もし等号も加えて$n \leq N - M = 4$であれば、$n = 4$まで物体をとれて、かつ$n =4$個の$b$をとると$a$は0なので$x = 0$です。逆に、$n \geq N - M = 4$だとすると、$n = 4$以上の物体をとることになります。$n = 4$では依然として$x = 0$になりうるのです。そのため$n > N - M$という条件であるので、参考の方にtypoの疑いがあるのです。

超幾何分布はこの時の確率分布です。組み合わせの計算により

$$\begin{align*} f(x) &= \frac{ {}_M C_x \cdot {}_{N - M} C_{n - x} }{ {}_N C_n } \\[8pt] x &= {\rm Max}(0, n - (N - M))), \ldots\ldots, {\rm Min}(n, M) \end{align*}$$

となります。

数値計算への導入

この分布を数値的に計算するためは組み合わせの数を計算しないといけません。しかし、組み合わせの数にでてくる数には階乗がふくまれるため、通常のIntやBigIntegerで計算してもたかが知れています。そこで対数に変換することで、比較的大きな数についての組み合わせの数を計算します。

対数にすることで計算を頑張る。コンビネーションは${}_n C_k$とすると

$$\begin{align*} {}_n C_k &= \frac{n!}{k! (n - k)!} \\[8pt] &= \prod_{i = 1}^k \frac{n - i + 1}{i} \end{align*}$$

です。両編に$\ln$をとると

$$\begin{align*} \ln {}_n C_k &= \ln \left( \prod_{i = 1}^k \frac{n - i + 1}{i} \right) \\ &= \sum_{i = 1}^k \left [ \ln (n - i + 1) - \ln i \right] \end{align*}$$

です。$\sum$で書けばプログラムに反映しやすくなります。

実装

下記では捕獲再捕獲法に関する例を計算したものです。セットアップとしては、ある湖に魚が1000匹いる状況を考えます。湖にいる魚のうち200匹を捕まえて、尻尾に赤い目印をつけて放流したとします。いま湖から魚を5匹獲ったとすると、赤い目印がついた魚が1匹のとき、0匹の時の確率はどれくらいか？という問題です。

import kotlin.math.ln
import kotlin.math.exp
import kotlin.math.min

/**
 * 二項係数の自然対数 ln(nCk)
 * Intの拡張関数とする
 */
fun Int.logCombination(k: Int): Double {
    if (k < 0 || k > this) return Double.NEGATIVE_INFINITY
    val kk = min(k, this - k) // 対称性を利用する
    return (1..k).sumOf { i ->
        ln((this - i + 1).toDouble()) - ln(i.toDouble())
    }
}

/**
 * 超幾何分布
 * N: ある湖の全ての魚（母集団）
 * M: 尻尾に赤い色の標識をつけて放流した魚（母集団の中の当たり）
 * n: 獲った魚の数（試行回数）
 * x: 標識がついた魚の数（当たりの数）
 */
fun hypergeometricProbability(
    N: Int, M: Int, n: Int, x: Int
): Double {
    // 定義域外で確率0
    if (x < 0 || x > n || x > M || n - x > N - M) {
        return 0.0
    }
    val logProb = M.logCombination(x) +
            (N - M).logCombination(n - x) -
            N.logCombination(n)

    return exp(logProb)
}


fun main() {
    // 超幾何分布
    // 母集団1000, 当たり200, 5回引いて, 1回当たる確率
    val prob1 = hypergeometricProbability(1000, 200, 5, 1)
    println("P(X=1) = $prob1")

    val prob0 = hypergeometricProbability(1000, 200, 5, 0)
    println("P(X=0) = $prob0")

    // 全確率の和がほぼ1になる
    var sumP = 0.0
    for(i in 0..5) {
        sumP += hypergeometricProbability(1000, 200, 5, i)
    }
    println("Sum of probabilities = $sumP")
}

これの計算結果は

P(X=1) = 0.41062695331123905
P(X=0) = 0.3268590548357458
Sum of probabilities = 0.9999999999999992

となり、５匹中１匹に色がついている確率が41%、0匹の確率が32%となり、実は１匹のほうが確率が高いのです。

また、分布を可視化してみると

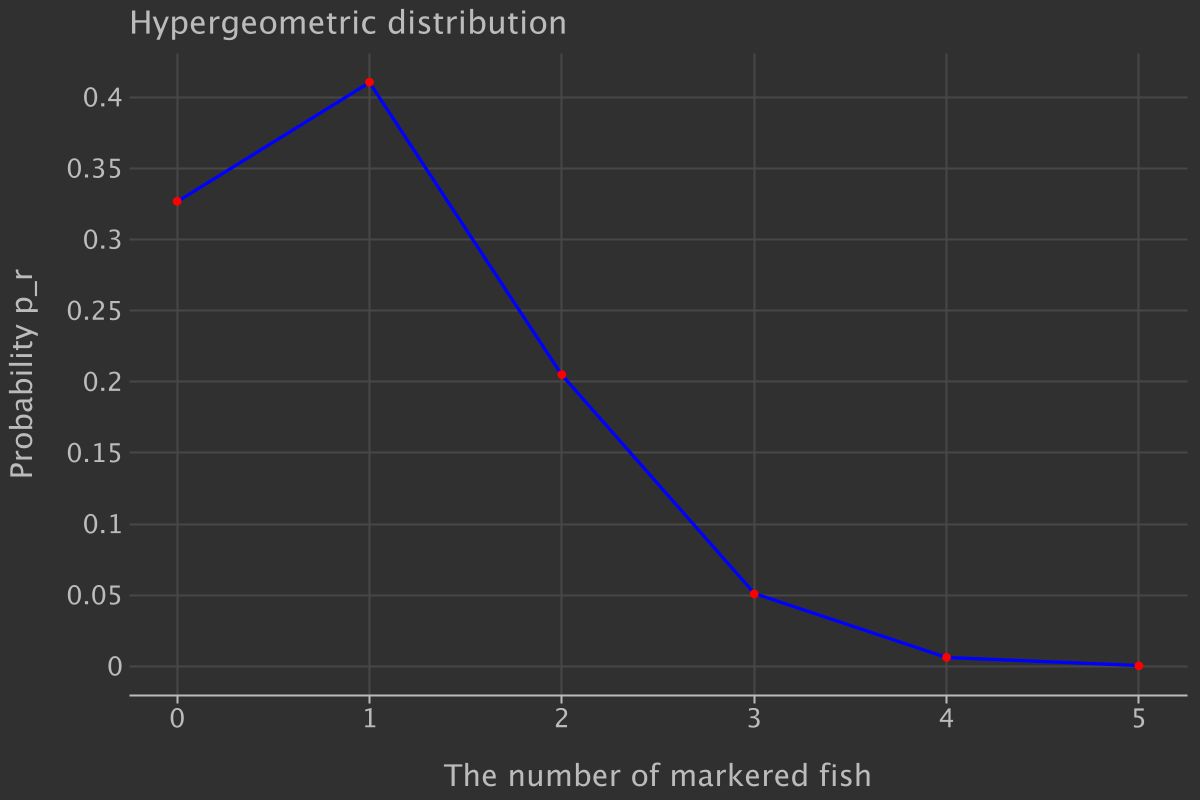
参考資料

統計学入門　東京大学教養学部統計学教室編 東京大学出版会 リポジトリ

更新履歴

• 2026-01-08: Kotlinの組み合わせの計算をKotlinらしく改善

Footnotes

1. 統計学入門　東京大学教養学部統計学教室編 東京大学出版会 ↩ ↩²